Before starting to explain Floyd algorithm, I want to compare Dijkstra algorithm with Floyd.
1. it is used only when we already know start node to all nodes
this means that source node should be single.
2. It will fail if graph has negative distance. distance or weight should be > 0
3. it is also called single-source shortest path or SSSP algorithm.
4. O(N^2)
Floyd-Warshall's algorithm
1. it is used to find all nodes to all nodes
2. This only fails when there are negative cycles.
3. O(N^3)
4. We can have one or more links of negative cost, c(x, y)<0,
Later on, I will Study Bellman-Ford and also post on blog.
1 let dist be a |V| × |V| array of minimum distances initialized to ∞ (infinity) 2 for each vertex v 3 dist[v][v] ← 0 4 for each edge (u,v) 5 dist[u][v] ← w(u,v) // the weight of the edge (u,v) 6 for k from 1 to |V| 7 for i from 1 to |V| 8 for j from 1 to |V| 9 if dist[i][j] > dist[i][k] + dist[k][j] 10 dist[i][j] ← dist[i][k] + dist[k][j] 11 end if
Code Explanation
1. line 3, define graph and initialize value. in my case Integer.max
2. line 5, set real weight of edge between two nodes.
3. find dist[i][j] through k node. .. repeatedly k = 1 to last node
find and set if dist[i][j] < dist[i][k] + dist[k][j], in other words, find minimum path and update minimum distance
Picture Explanation
continue and continue.....
.............
.......
...
.
Finally we get shorted graph from all nodes to all node
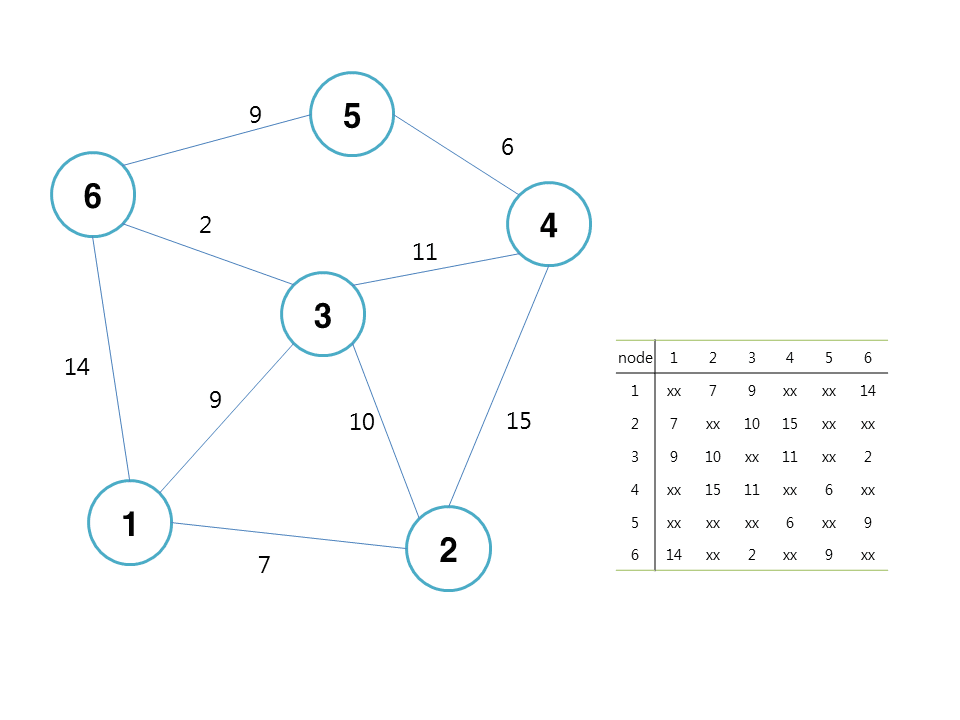
Last time, I wrote about shortest path by using dijkstra, with above graph.
at that time, test case was 1 to 5 , and result is 20.
and also this result by using floyd is the same as using dijkstra.
at that time, test case was 1 to 5 , and result is 20.
and also this result by using floyd is the same as using dijkstra.
below is my java code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 | package mybook; import java.util.Arrays; public class FloydWarshall { public int[][] graph ; public final int INFINITY =Integer.MAX_VALUE; public static void main(String[] args) { // TODO Auto-generated method stub FloydWarshall floyd = new FloydWarshall(); floyd.init(); floyd.printValue(floyd.graph); floyd.start(); System.out.println(); floyd.printValue(floyd.graph); } private void start() { for(int k=1; k<7; k++){ for(int i=1; i<7; i++){ for(int j=1; j<7; j++){ if(graph[i][k]!= INFINITY && graph[k][j] != INFINITY && i != j){ System.out.println(); System.out.println("from : " + i + ", center : " + k + ", to : " + j); if(graph[i][j] > graph[i][k] + graph[k][j]){ graph[i][j] = graph[i][k] + graph[k][j]; } //System.out.println("[" +i + "]["+j +"] : " + graph[i][j] ); printValue(graph); } } } } } public void init(){ int count = 7; graph = new int [count][count]; printValue(graph); int len =graph.length; for(int i=0; i<len; i++){ for(int j =0; j<len; j++){ graph[i][j] = INFINITY; } } printValue(graph); setvalue(graph, 1, 3, 9); setvalue(graph, 1, 2, 7); setvalue(graph, 1, 6, 14); setvalue(graph, 2, 3, 10); setvalue(graph, 2, 4, 15); setvalue(graph, 3, 4, 11); setvalue(graph, 3, 6, 2); setvalue(graph, 4, 5, 6); setvalue(graph, 5, 6, 9); } public void setvalue(int [][] graph, int start, int end, int val){ graph[start][end] = val; graph[end][start] = val; } public void printValue(int graph[][]){ for(int i=1; i<graph.length; i++){ for(int j=1; j< graph.length; j++){ String pr = ""; int val = graph[i][j]; if(0< val && val < 10){ pr = "0"+ val; }else{ if(val == Integer.MAX_VALUE){ System.out.print("xx"); System.out.print(pr + " "); continue; } pr = val +""; } System.out.print(pr + " "); } System.out.println(); } } } |
if you have any question Comment Please~






No comments:
Post a Comment