Programming is my life~! : Dijkstra's algorithm in java

Today I want to post Dijkstra Algorithm.

Dijkstra Algorithm is used to find shortest path.
this algorithm is well-known because many applications which programmed by this algorithm we are using in practice.

Usage,
Subway Map, GeoGraphic Infomation System and so on.

Before posting this algorithm, I had to study many things to understand for this one.

# List #

1. BFS(Breadth-First-Search),
2. DFS(Depth-First-Search),
3. Prim algorithm,
4. Union Find algorithm,
5. Kruskal algorithm,
6. Topology algorithm,

After writing those code in Java, I was able to totally understand Dijkstra Algorithm, usages where to use and how to customizing,

Pseudocode

 1  function Dijkstra(Graph, source):
 2
 3      dist[source] ← 0                       // Distance from source to source
 4      prev[source] ← undefined               // Previous node in optimal path initialization
 5
 6      for each vertex v in Graph:  // Initialization
 7          if v ≠ source            // Where v has not yet been removed from Q (unvisited nodes)
 8              dist[v] ← infinity             // Unknown distance function from source to v
 9              prev[v] ← undefined            // Previous node in optimal path from source
10          end if 
11          add v to Q                     // All nodes initially in Q (unvisited nodes)
12      end for
13      
14      while Q is not empty:
15          u ← vertex in Q with min dist[u]  // Source node in first case
16          remove u from Q 
17          
18          for each neighbor v of u:           // where v has not yet been removed from Q.
19              alt ← dist[u] + length(u, v)
20              if alt < dist[v]:               // A shorter path to v has been found
21                  dist[v] ← alt 
22                  prev[v] ← u 
23              end if
24          end for
25      end while
26
27      return dist[], prev[]
28
29  end function

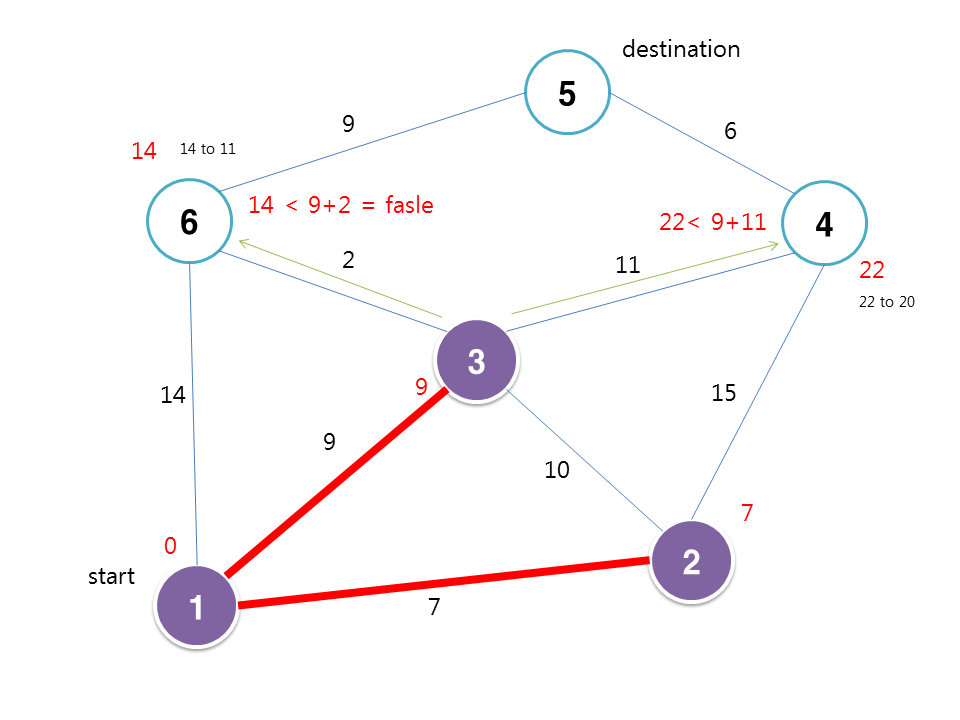
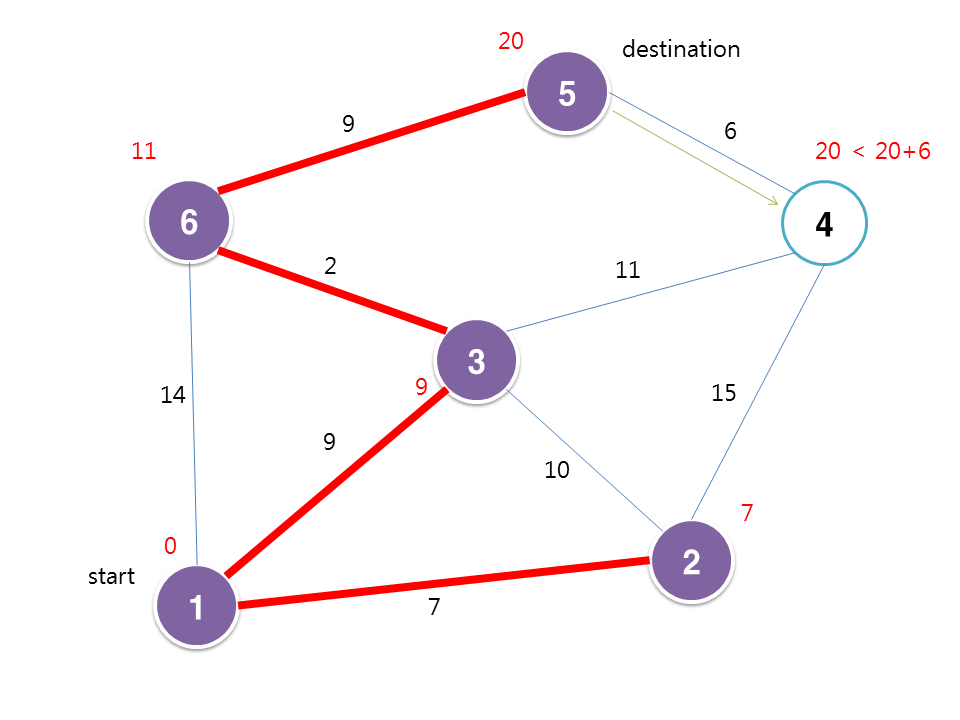
this is graph start from node 1

check length (weight)

visit node 2 (minimu length from visited to none visited)

and check neighbors length

visit 3

visit 6

this is what shortest path

and I will show you my java code and this has two testcase

firstcase is from wekipedia

http://en.wikipedia.org/wiki/Dijkstra's_algorithm

secondcase is from geeksforgeeks

http://www.geeksforgeeks.org/greedy-algorithms-set-6-dijkstras-shortest-path-algorithm/

if you like....

if you have question...

if you found something is strange...

Comment plz~

package mybook;
import java.util.Arrays;
import java.util.HashSet;
import java.util.Iterator;

public class DijkstraTest {
 
 int[][] graph ;
 int[][] dijsktraGraph ;
 int[] dist;
 int[] previous;
 int startPosition ;
 
 // visited node
 HashSet<Integer> used = new HashSet<Integer>();

 // not visited node
 HashSet<Integer> notUsed = new HashSet<Integer>();
 
 public static void main(String[] args){
  DijkstraTest prim = new DijkstraTest();
  prim.secondCaseInit();
  prim.start();
  prim.printValue(prim.dijsktraGraph);
  
  // first test
  // find shortest path from start node
  prim.printPath(1);
  prim.printPath(2);
  prim.printPath(3);
  prim.printPath(4);
  prim.printPath(5);
  prim.printPath(6);
  
  
  // second  test
  prim.firstCaseInit(); 
  prim.start();
  prim.printValue(prim.dijsktraGraph);
  prim.printPath(1);
  prim.printPath(2);
  prim.printPath(3);
  prim.printPath(4);
  prim.printPath(5);
  prim.printPath(6);
  prim.printPath(8);
 }
 
 public void start(){
  // start vertex(node) should be set in advance.
  notUsed.remove(startPosition);
  used.add(startPosition);
  checkWeight(startPosition);
  
  while (! notUsed.isEmpty()) {
   // find shortest distance from used usedNode to targetNode
   int [] node = minimumNode();
   int targetNode = node[1];
   
   // remove target from Queue
   notUsed.remove(targetNode);
   used.add(targetNode);
   
   // draw graph
   dijsktraGraph[node[0]][node[1]]=1;
   
   // check new weight to neighbors of target
   checkWeight(targetNode);
  }
 }
 
 
 /**
  * check the new distances of neighbors of the targetNode if graph[u][v] + dist[u] < dist[v]
  * 
  *  u = from 
  *  v = t
  *  
  * @param u
  */
 public void checkWeight(int u){
  for(int v=startPosition+1; v<graph.length; v++){
   if(graph[u][v] > 0){
    if((dist[v] ==0) || notUsed.contains(v) && graph[u][v] + dist[u] < dist[v] ){
     dist[v] = graph[u][v] + dist[u];
     // chase for the shortest way
     previous[v] = u;
    }
   }
  }
  System.out.println(Arrays.toString(dist));
 }

 /**
  * find targetnode which has min weight in from used node to notUsed node
  * 
  * @return node[from][to]
  */
 private int[] minimumNode() {
  int minValue = Integer.MAX_VALUE;
  int[] node = new int[2];
  
  Iterator<Integer> uI = used.iterator();
  while(uI.hasNext()){
   int used = uI.next();
   
   Iterator<Integer> nI = notUsed.iterator();
   while(nI.hasNext()){
    int notUsed = nI.next();
    if(graph[used][notUsed] > 0){
     int distance = dist[used] + graph[used][notUsed]; 
     if( distance < minValue){
      minValue = distance;
      node[0]= used;
      node[1] = notUsed;
     }
    }
   }
  }
  return node;
 } 
 
 public void setvalue(int [][] graph, int start, int end, int val){
  graph[start][end] = val;
  graph[end][start] = val;
 }
 
 public  void printValue(int graph[][]){
  for(int i=0; i<graph.length; i++){
   for(int j=0; j< graph.length; j++){
    
    String pr = "";
    int val = graph[i][j];
    if(val < 10){
     pr = "0"+ val; 
    }else{
     pr = val +"";
    }
    System.out.print(pr + " ");
   }
   System.out.println();
  }
 }
 
 public void firstCaseInit(){
  int count = 9;
  
  graph = new int [count][count];
  dijsktraGraph = new int [count][count];
  dist = new int[count];
  previous = new int[count];
  startPosition = 0;
   
   used= new HashSet<Integer>();
   notUsed= new HashSet<Integer>();
  
  setvalue(graph, 0, 1, 4);
  setvalue(graph, 0, 7, 8);
  setvalue(graph, 1, 7, 11);
  setvalue(graph, 1, 2, 8);
  setvalue(graph, 2, 8, 2);
  setvalue(graph, 8, 6, 6);
  setvalue(graph, 6, 7, 1);
  setvalue(graph, 7, 8, 7);
  setvalue(graph, 2, 3, 7);
  setvalue(graph, 2, 5, 4);
  setvalue(graph, 5, 6, 2);
  setvalue(graph, 3, 5, 14);
  setvalue(graph, 3, 4, 9);
  setvalue(graph, 4, 5, 10);
  
  for(int i=startPosition; i<count; i++){
   notUsed.add(i); 
  }
 }
 
 public void secondCaseInit(){
  int count = 7;
  
  graph = new int [count][count];
  dijsktraGraph = new int [count][count];
  dist = new int[count];
  previous = new int[count];
  
  startPosition = 1;
  
  used= new HashSet<Integer>();
  notUsed= new HashSet<Integer>();
  
  setvalue(graph, 1, 3, 9);
  setvalue(graph, 1, 2, 7);
  setvalue(graph, 1, 6, 14);
  setvalue(graph, 2, 3, 10);
  setvalue(graph, 2, 4, 15);
  setvalue(graph, 3, 4, 11);
  setvalue(graph, 3, 6, 2);
  setvalue(graph, 4, 5, 6);
  setvalue(graph, 5, 6, 9);
  
  for(int i=startPosition; i<count; i++){
   notUsed.add(i); 
  }
 }
 
 private void printPath(int i) {
  if(i != startPosition){
   System.out.print(i + "to " + previous[i] + ", ");
   printPath(previous[i]);
  }else{
   System.out.println(i + " is last ");
  }
 }
}

Programming is my life~!

Thursday, January 15, 2015

Dijkstra's algorithm in java

No comments:

Post a Comment