Thursday, January 8, 2015

Kruskal Algorithm in java

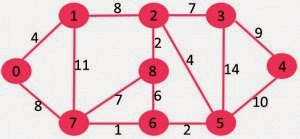
Today I explain Kruskal algorithm

From the logic I coded in java.

This is another way to find minimum spanning this.
before you read this post, prerequisite is understanding Union and Find Algorithm.
I worte last post Union and Find Algorithm. 

and you can read Prim algorithm.

the logic is below.

1. setting nodes, changing nodes to subsets;
2. sort edges order by weight ascending
3. and Use Union and Find Algorithm.

if my code is show how stange. reply and discuss











Reference:


my java code is



  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
package mybook;
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.HashSet;
import java.util.Iterator;
import java.util.LinkedList;

public class Kruskal {
 /**
  * all edges
  */
 ArrayList<Edge> edges= new ArrayList<Edge>();
 
 ArrayList<ItemNode> nodes= new ArrayList<ItemNode>();
 ArrayList<HashSet<ItemNode>> subsets = new ArrayList<HashSet<ItemNode>>();
 
 public static void main(String args[]){
  Kruskal kruskal= new Kruskal();
  kruskal.init();
  

 }
 
 public void init(){
  // setting nodes;
  nodes.add(new ItemNode(0));
  nodes.add(new ItemNode(1));
  nodes.add(new ItemNode(2));
  nodes.add(new ItemNode(3));
  nodes.add(new ItemNode(4));
  nodes.add(new ItemNode(5));
  nodes.add(new ItemNode(6));
  nodes.add(new ItemNode(7));
  nodes.add(new ItemNode(8));
  
  // setting edges;
  edges.add(new Edge(0,1,4));
  edges.add(new Edge(0,7,8));
  edges.add(new Edge(1,2,8));
  edges.add(new Edge(1,7,11));
  edges.add(new Edge(2,8,2));
  edges.add(new Edge(2,3,7));
  edges.add(new Edge(2,5,4));
  edges.add(new Edge(3,4,9));
  edges.add(new Edge(3,5,14));
  edges.add(new Edge(4,5,10));
  edges.add(new Edge(5,6,2));
  edges.add(new Edge(6,7,1));
  edges.add(new Edge(6,8,6));
  edges.add(new Edge(7,8,7));
  
  // make nodes to subsets
  for(int i=0; i<nodes.size(); i++){
   HashSet<ItemNode> set = new HashSet<ItemNode>();
   set.add(nodes.get(i));
   subsets.add(set);
  }
  
  // sort
  Collections.sort(edges, new CustomComparator());
  
  System.out.println(edges);
  
  
  // union and find algorithm
  for(int i=0; i<edges.size(); i++){
   Edge edg = edges.get(i);
   ItemNode srcNode = nodes.get(edg.src);
   ItemNode destNode = nodes.get(edg.dest);
   
   if(find(srcNode) == find(destNode)){
    // same subsets
   }else{
    System.out.println( edg.src + " > " + edg.dest);
    union(find(srcNode), find(destNode));
   }
  }
 }
 
 public void union(int aSubset, int bSubset){
  HashSet<ItemNode> aSet = subsets.get(aSubset);
  HashSet<ItemNode> bSet = subsets.get(bSubset);
  
  Iterator<ItemNode> iter = bSet.iterator();
  while(iter .hasNext()){
   ItemNode b = iter.next();
   aSet.add(b);
//   System.out.println(bSet.size());
//   System.out.println("bnumber : " + b.number);
  }
  subsets.remove(bSubset);
  printSet();
  
 }
 
 public void printSet(){
  
  for(int i=0;i<subsets.size(); i++){
   HashSet<ItemNode> hashSet= subsets.get(i);
   
   Iterator<ItemNode> iter= hashSet.iterator();
   System.out.print("{");
   while(iter.hasNext()){
    ItemNode node = iter.next();
    System.out.print(node.number + ",");
   }
   System.out.print("}");
   
  }
  System.out.println();
 }
 
 public void setvalue(int [][] graph, int start, int end, int val){
  graph[start][end] = val;
  graph[end][start] = val;
 }
 class ItemNode {
  boolean isRoot = true;
  int number = 0;
  LinkedList<ItemNode> subnodes= new LinkedList<ItemNode>();
  ItemNode parendNode = null;
  
  ItemNode(int number){
   this.number = number;
  }
 }
 
 
 public int  find(ItemNode node){
  int number=-1;
  
  for(int i=0; i<subsets.size(); i++){
   HashSet<ItemNode> set = subsets.get(i);
   Iterator<ItemNode> iterator = set.iterator();
   while(iterator.hasNext()){
    ItemNode setnode = iterator.next();
    if(setnode.number == node.number){
     number= i;
     return number;
    }
    
   }
  }
  return number;
 }
}
class CustomComparator implements Comparator<Edge>{

 @Override
 public int compare(Edge o1, Edge o2) {
  return o1.weight - o2.weight;
 }
}

class Edge{
 int src;
 int dest; 
 int weight;
 
 Edge(int src, int dest, int weight){
  this.src = src;
  this.dest = dest;
  this.weight = weight;
 }
 @Override
 public String toString() {
  return "Edge [src=" + src + ", dest=" + dest + ", weight=" + weight
    + "] \n";
 }
}
-
Labels:

1 comment:

Subscribe to: Post Comments (Atom)